二分查找

注意：排序数组中的搜索问题，首先想到二分法。

一、基本的二分查找

最简单的情况就是搜索一个数，如果存在，返回索引；否则返回-1。

func search(nums []int, target int) int {
    // 二分查找
    left, right := 0, len(nums) - 1 // 注意
    for left <= right {
        mid := left + (right - left) >> 1 // 注意
        if nums[mid] == target {
            return mid
        } else if nums[mid] > target {
            right = mid - 1 // 注意
        } else if nums[mid] < target {
            left = mid + 1 // 注意
        }
    }
    return -1
}

mid防止溢出

代码mid := left + (right - left) >> 1目的是为了防止left和right太大相加导致溢出。

循环结束条件

循环结束条件是<=，而不是<。

是因为初始化right的赋值是nums.length - 1，即最后一个元素的索引，而不是nums.length。两者出现在不同功能的二分查找中，区别是：前者相当于两端都是闭区间[left, right]，后者相当于左闭右开区间[left, right)。我们可以把这个区间称作搜索区间。而搜索未找到停止搜索的条件就是搜索区间为空。当left == right时，搜索区间还有一个值。所以循环结束条件是<=。

left、right每次迭代更替的值

此处是left = mid + 1, right = mid - 1,有时候是right = mid或者left = mid。为什么呢？

当我们理解搜索区间的概念后，本算法中搜索区间两端都是闭的。当发现索引mid不是要找的target时，下一步的搜索区间应该是[left, mid - 1]或者[mid + 1, right]。因为mid已经搜索过，应该从搜索区间中去除。

二、搜索左边界

常见代码如下：

func search(nums []int, target int) int {
  	if len(nums) == 0 {
    		return -1
  	}
    left, right := 0, len(nums) // 注意
    for left < right { //注意
        mid := left + (right - left) >> 1
        if nums[mid] == target {
            right = mid
        } else if nums[mid] > target {
            right = mid // 注意
        } else if nums[mid] < target {
            left = mid + 1
        }
    }
    return left
}

循环结束条件

此处终止条件是left < right。是因为前面right = nums.length，所以搜索区间是[left, right)左闭右开。所以循环的终止条件等价于left == right，此时搜索区间已经为空，可以终止。

注意：至于为什么这里写成左闭右开搜索区间形式，是因为这种写法较为普遍。也可以赋值为right = nums.length - 1写为闭区间。

返回值解惑

• 为什么没有返回-1操作？如果nums中不存在target这个值，怎么办？

先理解左侧边界有什么特殊含义：

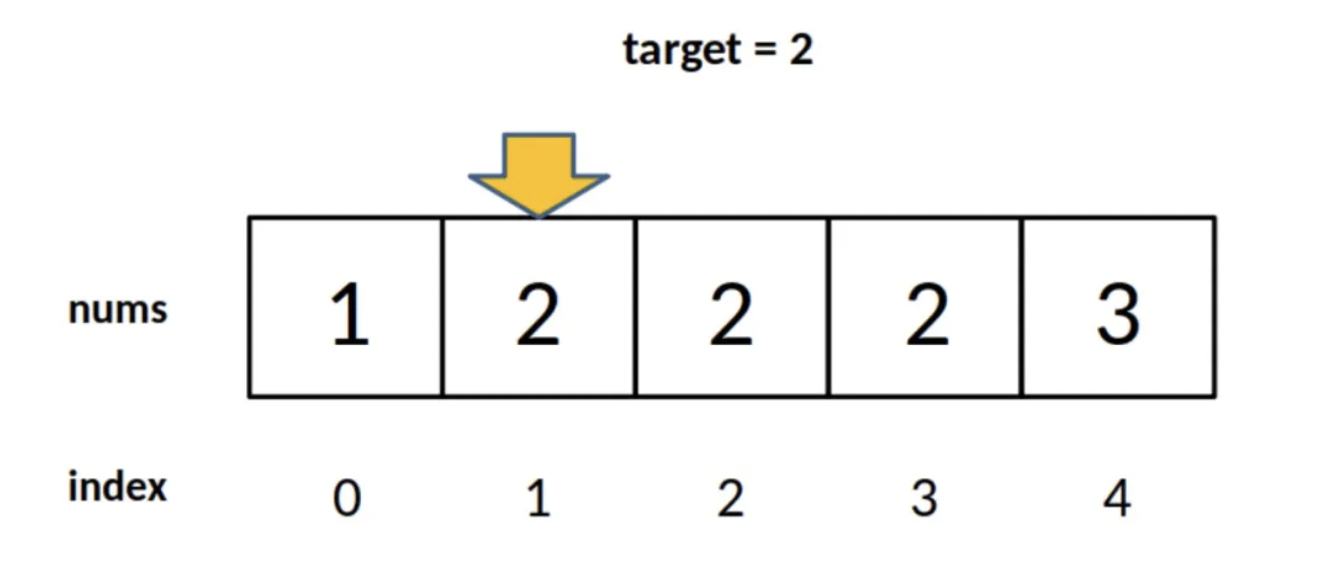
对于上述数组，算反会返回1。这个1的含义可以解读为：nums中小于2的元素有1个。

比如对于有序数组nums = [2,3,5,7],target = 1，算法会返回0，含义是：nums中小于1的元素有0个。

再比如说nums = [2,3,5,7],target = 8，算法会返回4，含义是：nums中小于8的元素有4个。

可以看出，函数返回值（即left变量的值）取值区间是闭区间[0, nums.length]。所以我们可以在循环结束后面添加如下代码，就能在正确的时候返回-1:

for left < right {
  // ...
}
// target 比所有数都大
if left == len(nums) {
  return -1
}
// 处理其他情况
if nums[left] == target {
  return left
} else {
  return -1
}

• 为什么返回left而不是right?

因为循环终止条件是left == right，所以都是一样的。

left、right每次迭代更替的值

此处right = mid， left = mid + 1是因为搜索区间是[left, right)左闭右开，所以当nums[mid]被检测之后，下一步搜索区间应该去掉mid分隔为两个区间，即[left, mid)和[mid + 1, right)。

为什么能搜索左侧区间？

关键在于对nums[mid] == target这种情况的处理：

找到target时不立即返回，而是缩小搜索区间的上届right，在区间[left, mid)中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

三、搜索右边界

和搜索左边界类似，依然采用左闭右开搜索区间的写法，有两处不同已标注：

func search(nums []int, target int) int {
  	if len(nums) == 0 {
    		return -1
  	}
    left, right := 0, len(nums)
    for left < right {
        mid := left + (right - left) >> 1
        if nums[mid] == target {
            left = mid + 1 // 注意
        } else if nums[mid] > target {
            right = mid
        } else if nums[mid] < target {
            left = mid + 1
        }
    }
    return left - 1 // 注意
}

为什么能搜索右侧区间？

类似的，关键点在于：

当nums[mid] == target时，不要立即返回，而是增大搜索区间的下界left,使得区间不断向右收缩，达到锁定右侧边界的目的。

返回值解惑

• 为什么最后返回left - 1而不像左侧边界的函数，返回left？而且我觉得这里既然是搜索右侧边界，应该返回right才对。

因为循环终止条件是left == right,所以left和right是一样的。

至于为什么要减一，是搜索右侧边界的一个特殊点，关键在这个条件判断：

因为我们对left的更新必须是left = mid + 1，而循环结束时，nums[left]一定不等于target了，而nums[left - 1]可能是target。

• 为什么没有返回-1操作？如果nums中不存在target这个值，怎么办？

类似搜索左边界，left的取值范围是[0, nums;length]，所以添加如下代码，可以正确返回-1:

for left < right {
  // ...
}
// target 比所有数都小
if left == 0 {
  return -1
}
// 处理其他情况
if nums[left - 1] == target {
  return left - 1
} else {
  return -1
}