二分查找LeetCode题目应用

Narcissus 收录于算法学习

2021-09-06 约 1170 字预计阅读 3 分钟

二分搜索问题泛化

把题目抽象出一个自变量x,一个关于x的函数f(x),以及一个目标值target。

同时，x,f(x),target必须满足以下条件：

f(x)必须是在x上的单调函数。
题目是让计算满足约束条件f(x) == target时的x的值。

具体问题可以结合下面的图思考：

运用二分搜索解决具体的算法问题，可以从以下代码框架着手思考：

具体来说，可以总结为以下几步：

确定x，f(x)，target分别是什么，并写出函数f的代码。
找到x的取值范围作为二分搜索的搜索区间，初始化left和right变量。
根据题目要求，确定应该搜索左边界还是右边界，写出代码。

具体LeetCode题目应用

1、珂珂吃香蕉

本题中x就是吃香蕉的速度,target就是能吃完所有香蕉，f(x)可以定义为在速度x下能否吃完香蕉，**显然f(x)是单调递增的。**思考图像如下：

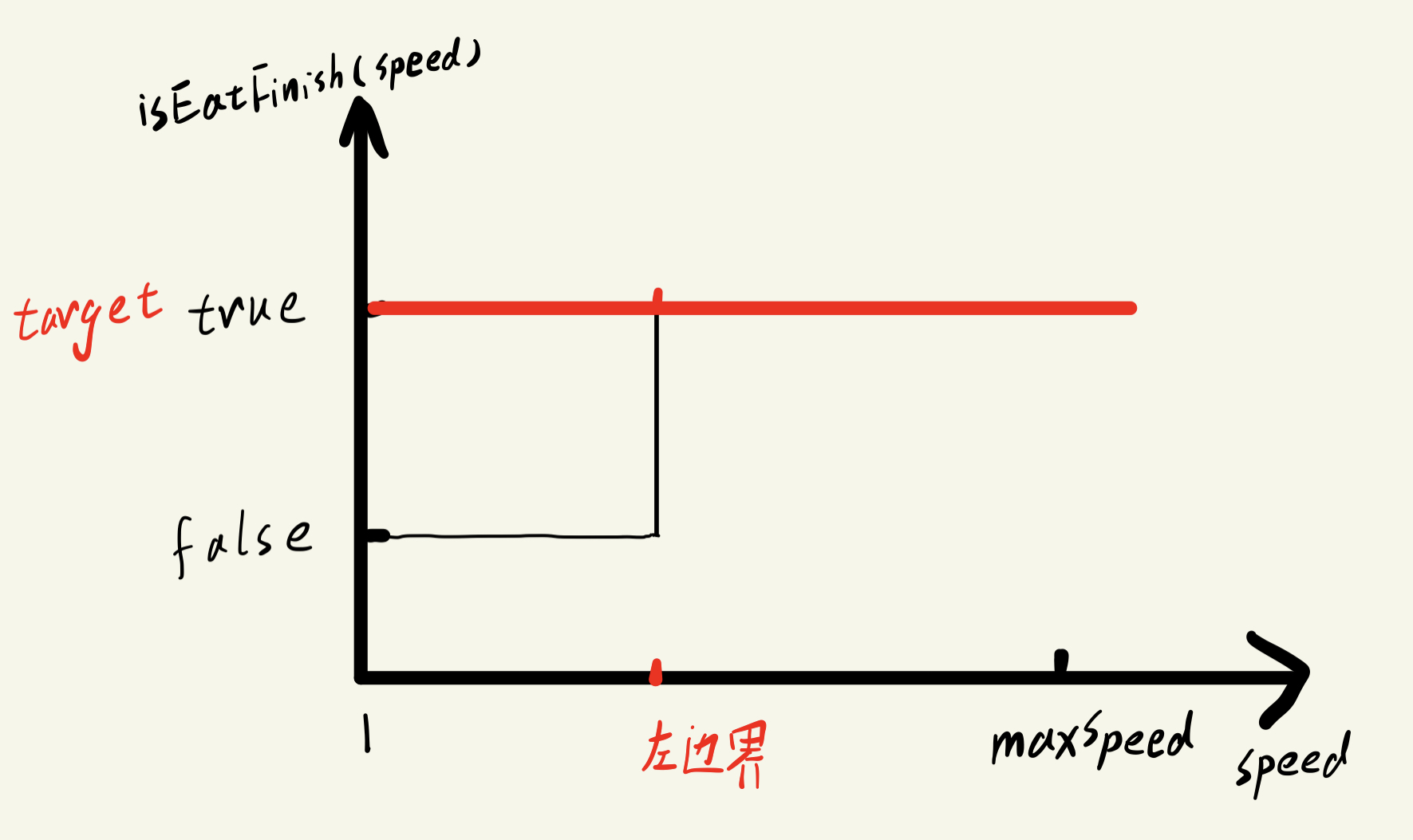
代码如下：

func minEatingSpeed(piles []int, h int) int {
    // 二分查找左边界
    maxSpeed := 0
    for _, val := range piles {
        if val > maxSpeed {
            maxSpeed = val
        }
    }
    left, right := 1, maxSpeed + 1
    for left < right {
        mid := left + (right - left) >> 1
        if isEatFinish(piles, h, mid) == true {
            right = mid
        } else {
            left = mid + 1
        }
    }
    return left
}

func isEatFinish(piles []int, h, speed int) bool {
    allTime := 0
    for _, pile := range piles {
        if pile % speed == 0 {
            allTime += pile / speed
        } else {
            allTime += (pile / speed) + 1
        }
    }
    return allTime <= h
}

2、运送货物

题目与上一道类似，x就是船载货能力,target就是能载完货物，f(x)可以定义为在载货能力x下能否载完货物。不做具体分析，代码如下：

func shipWithinDays(weights []int, days int) int {
    // 二分查找左边界
    maxWeight, sum := 0, 0
    for _, val := range weights {
        sum += val
        if val > maxWeight {
            maxWeight = val
        }
    }
    left, right := maxWeight, sum + 1
    for left < right {
        mid := left + (right - left) >> 1
        if isFinish(weights, days, mid) == true {
            right = mid
        } else {
            left = mid + 1
        }
    }
    return left
}

func isFinish(weights []int, day, cap int) bool {
    allDay, sumWeight := 0, 0
    for _, weight := range weights {
        if sumWeight + weight <= cap {
            sumWeight += weight
        } else {
            sumWeight = weight
            allDay++
        }
    }
    allDay++
    return allDay <= day
}

3、分隔数组的最大值

想用二分查找技巧优化算法，首先要把for循环形式的暴力算法写出来，如果算法中存在以下形式的for循环：

如果func(i)函数是在i上单调的函数，一定可以使用二分查找技巧优化for循环。

题目如下：

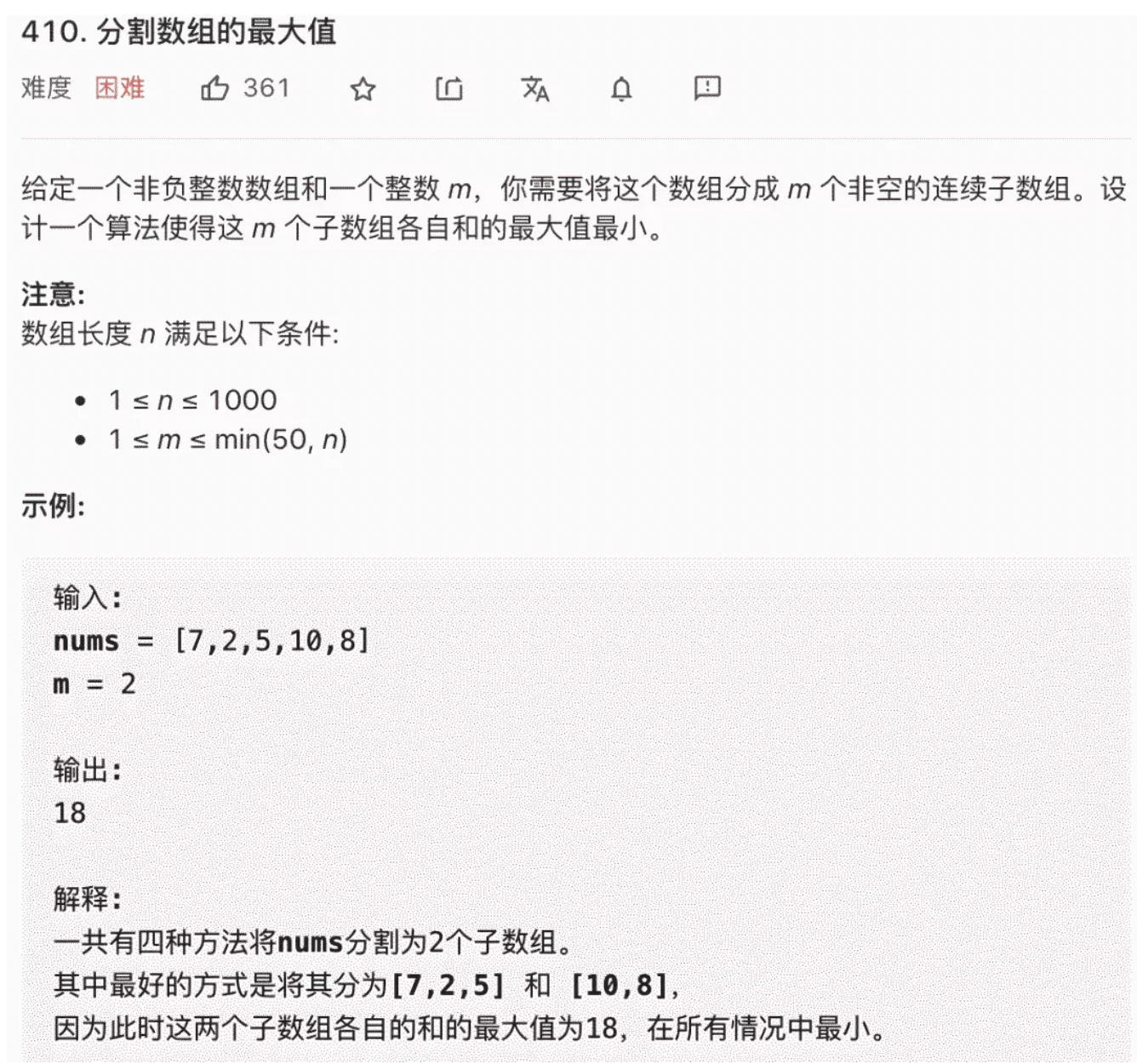
本题是固定m的值，让我们确定一个最大子数组和；我们可以反向思考，限制一个最大子数组和max，来反推最大子数组和为max时，至少可以将nums分割成几个子数组。这样我们可以写一个这样的split函数：

这样x就是max，函数就是split(max)，并且这个函数随max增大而减少，target就是m。找到满足m的最小的max值，即寻找左侧边界。

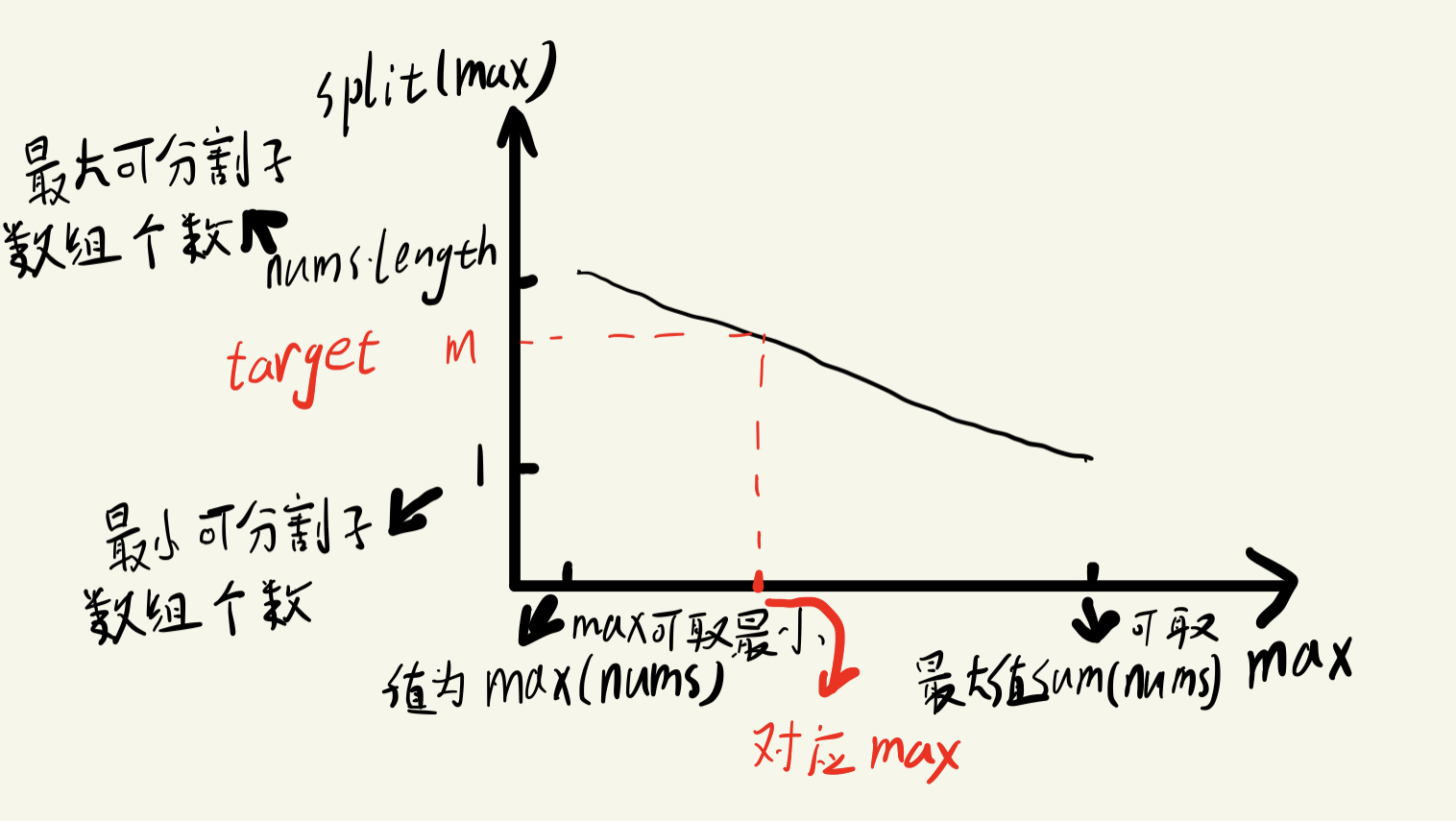
这样就转换为了二分查找左侧边界问题。代码如下：

func splitArray(nums []int, m int) int {
    // 二分查找左边界
    maxNum, sumNum := 0, 0
    for _, val := range nums {
        sumNum += val
        if val > maxNum {
            maxNum = val
        }
    }
    left, right := maxNum, sumNum + 1
    for left < right {
        mid := left + (right - left) >> 1
        if split(nums, mid) <= m {
            right = mid
        } else if split(nums, mid) > m {
            left = mid + 1
        }
    }
    return left
}

// 子数组和不超过max情况下，最少能分割为几个子数组，返回个数
func split(nums []int, max int) int {
    // 贪心思想解决
    sum, count := 0, 0
    for _, val := range nums {
        if sum + val <= max {
            sum += val
        } else {
            sum = val
            count++
        }
    }
    return count + 1
}

目录