刷题技巧总结

2022-03-05 约 2305 字预计阅读 5 分钟

位掩码技巧

原理讲解

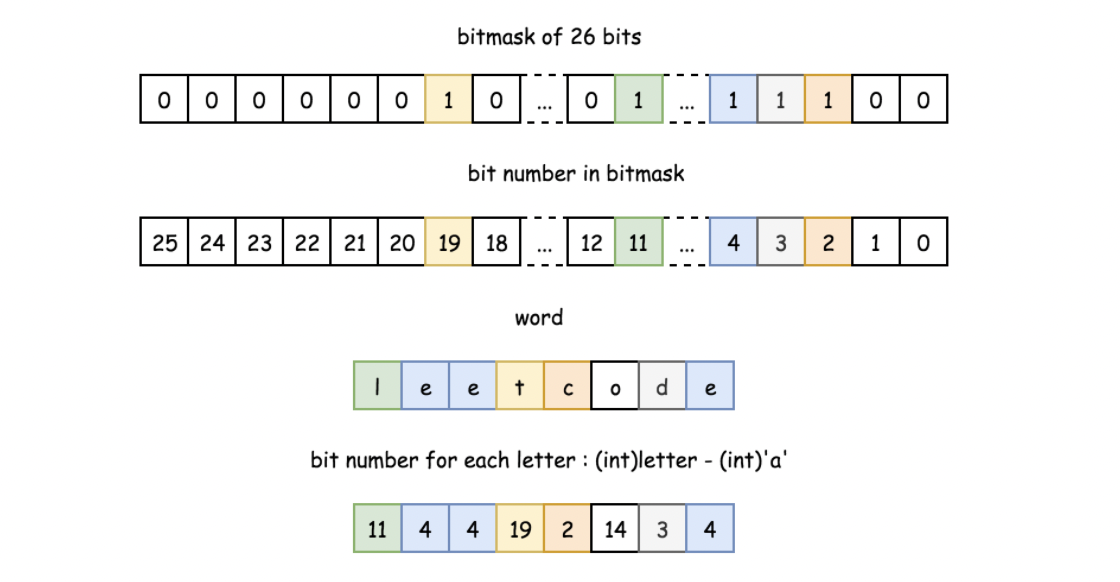
用于快速判断是否有重复出现的字符。限制条件为必须均为小写字母构成(不是必须)，则可以使用位掩码技巧：用一个(长度为26比特位，1表示含有该字母，0表示不含有)数存储字符串包含字母情况，则判断两个字符串可以通过两个位掩码数与计算是否为0(num1 & num2 == 0 ?)。

如何设置掩码的第 n 位？使用标准的位操作：n_th_bit = 1 << n。

如何计算一个单词的位掩码？遍历单词的每个字母，计算该字母在掩码中的位置 n = (int)ch - (int)'a'，然后创建一个第 n 位为 1 的掩码 n_th_bit = 1 << n，通过或操作将该码合并到位掩码中 bitmask |= n_th_bit。

LeetCode例题

代码如下：

func maxProduct(words []string) int {
    // 双循环
    // 判断两个单词是否有相同字母，用位掩码
    result, n := 0, len(words)
    bitsWords := make([]int, n)
    for i := 0; i < n; i++ {
        length := len(words[i])
        temp := 0
        for j := 0; j < length; j++ {
            t := int(words[i][j] - 'a')
            temp |= 1 << t
        }
        bitsWords[i] = temp
    }
    for i := 0; i < n - 1; i++ {
        for j := i + 1; j < n; j++ {
            if bitsWords[i] & bitsWords[j] == 0 {
                result = max(result, len(words[i]) * len(words[j]))
            }
        }
    }
    return result
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

回文串中心扩展技巧

计算有多少个回文子串的最朴素方法就是枚举出所有的回文子串，而枚举出所有的回文字串又有两种思路，分别是：

枚举出所有的子串，然后再判断这些子串是否是回文，复杂度为O(n^3)
枚举每一个可能的回文中心，然后用两个指针分别向左右两边拓展，当两个指针指向的元素相同的时候就拓展，否则停止拓展，复杂度可以降低到O(n^2)

注意考虑单个中心和两个中心的情况

func countSubstrings(s string) int {
    // 中心扩展
    n := len(s)
    result := 0
    for i := 0; i < n; i++ {
        result += getCount(s, n, i)
    }
    return result
}

func getCount(s string, n, index int) int {
    count := 1
    // 单中心
    left, right := index-1, index+1
    for left >= 0 && right < n {
        if s[left] != s[right] {
            break
        }
        count++
        left--
        right++
    }
    // 双中心
    left, right = index, index+1
    for left >= 0 && right < n {
        if s[left] != s[right] {
            break
        }
        count++
        left--
        right++
    }
    return count
}

前缀树(Trie)技巧

前缀树又叫字典树，英文名是Trie。就是一个像字典的树。用于快速查询「某个字符串/字符前缀」是否存在的数据结构。实现方面有两种方式：二维数组和TrieNode结构节点。

TrieNode结构节点实现代码：

type Trie struct {
    // 26叉树实现
    child [26]*Trie
}


/** Initialize your data structure here. */
func Constructor() Trie {
    return Trie{}
}


/** Inserts a word into the trie. */
func (this *Trie) Insert(word string)  {
    p := this
    for i := 0; i < len(word); i++ {
        if p.child[int(word[i]-'a')] == nil {
            node := &Trie{}
            p.child[int(word[i]-'a')] = node
        }
        p = p.child[int(word[i]-'a')]
    }
}

注意：节点结构体除了包含子节点外，可以包含isEnd标志符标志是否是某个单词结尾，也可以设定count统计叶子节点数目，用于判断当前节点是否是叶子节点。

缺点

前缀树在算法上是很常见的一种数据结构，但有如下不足：

字符集大小不好确定，上述题目只考虑了26个小写字母。
个别超长字符会使Trie进一步变深，如果 Trie 是存储在硬盘中，Trie 结构过深带来的影响是多次随机 IO，随机 IO 是成本很高的操作。
同时 Trie 的特殊结构，也会为分布式存储将会带来困难。

二分查找中小技巧

计算mid时避免溢出

mid := left + (right-left)>>1
mid = int(uint(left+right) >> 1) 官方源代码sort.Search()方法中使用的。

2. Sort.Search()使用

func Search(n int, f func(int) bool) int函数采用二分搜索找到区间[0, n)内最小的满足f(i) == true的i值。

源代码如下：

最小堆、最大堆技巧

在用heap包实现最小堆、最大堆时，有一些额外的技巧。主要是一些函数的使用场景总结：

1. Init(h Interface)函数

该函数作用是初始化堆，复杂度为O(n)。

一般创建堆后，如果需要一个一个插入的场景，则使用Push()即可，但对于需要一次插入多个元素时，可以先一次性插入，在调用Init()函数即可。

如下面官方文档中的优先队列使用示例：

2. Fix(h Interface, i int)函数

在修改第i个元素后，调用本函数修复堆，比删除第i个元素后插入新元素更有效率。复杂度O(log(n))，其中n等于h.Len()。

3. Remove(h Interface, i int) interface{}函数

删除堆中的第i个元素，并保持堆的约束性。复杂度O(log(n))，其中n等于h.Len()。

注意：删除的第i个元素是排序后的第i个，所以可用于删除堆中第几小(大)的元素。

即Pop(h)等价于Remove(h, 0)。

KMP算法

如果是暴力匹配过程：每一次子串都需要回退到第一个字符，而被匹配的串要回退到开始匹配位置的下一个位置，重新开始匹配。

KMP算法是一种字符串匹配算法，可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。

next数组

next数组是对于模式串而言的。模式串P的next数组定义为：next[i] 表示 P[0] ~ P[i] 这一个子串，使得前k个字符恰等于后k个字符的最大的k。

注意：k不能取i+1，因为子串一共有i+1个字符，自己和自己相等，没有意义。

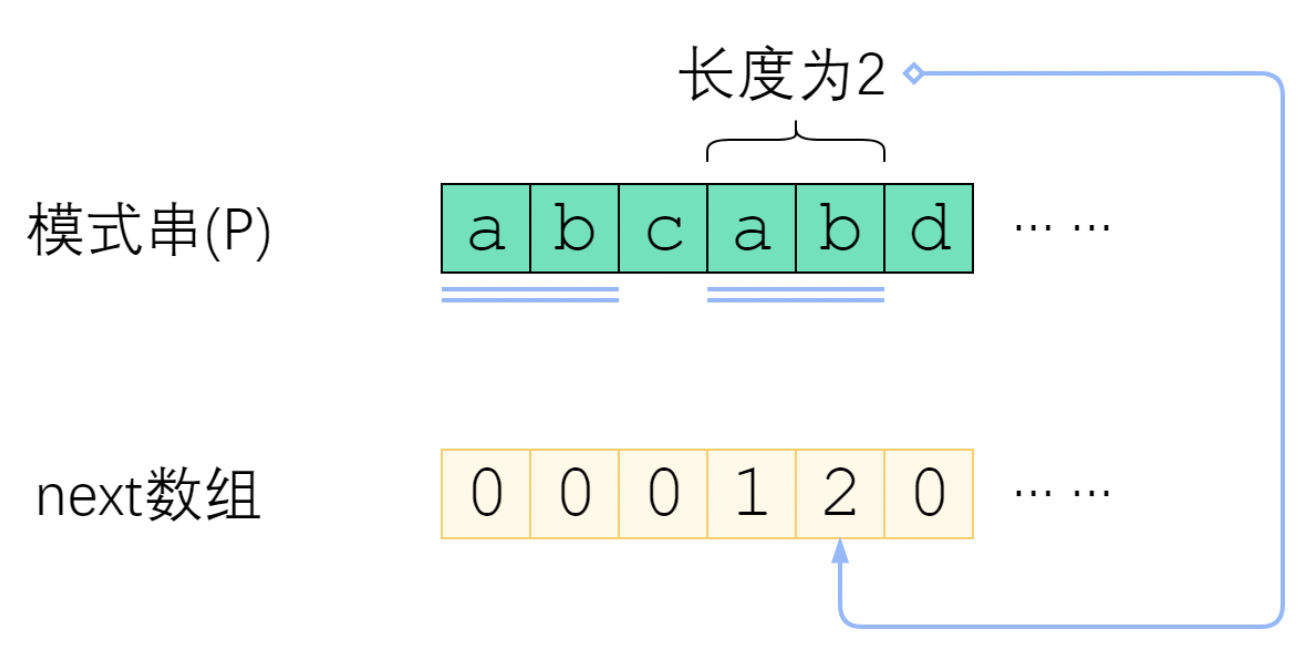
2. 快速构建next数组

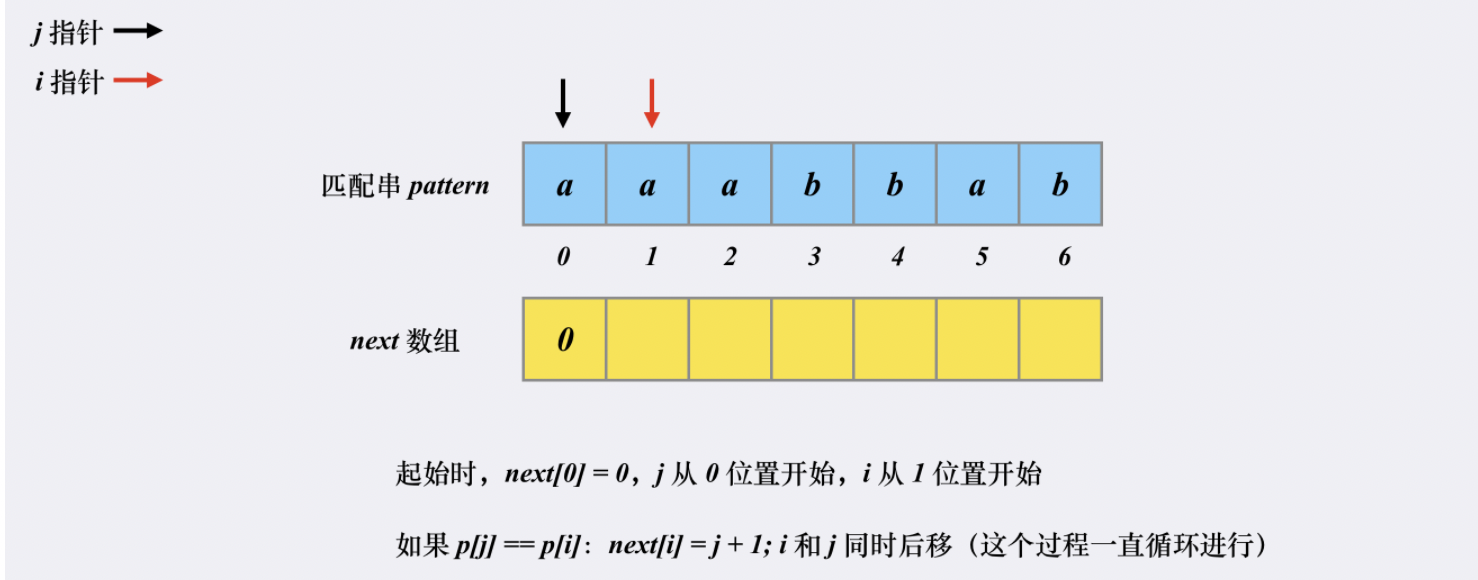
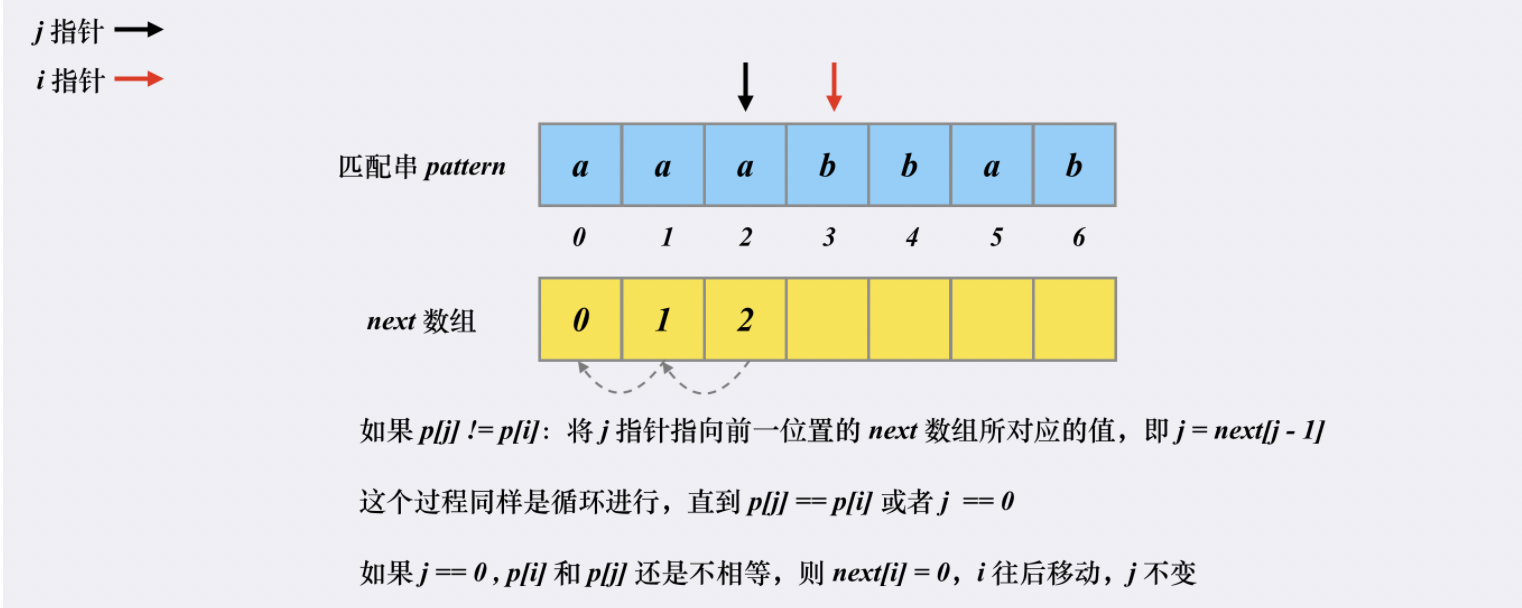
快速构建next数组也是匹配的过程：

calcMaxMatchLengths := func(s []byte) []int {
		next := make([]int, len(s))
		for i, c := 1, 0; i < len(s); i++ {
			v := s[i]
			for c > 0 && s[c] != v {
				c = next[c-1]
			}
			if s[c] == v {
				c++
			}
			next[i] = c
		}
		return next
	}

使用next数组进行匹配

如果出现不匹配情况，则会检查之前已经匹配成功的部分中里是否存在相同的「前缀」和「后缀」。如果存在，则跳转到「前缀」的下一个位置继续往下匹配。