排序

Narcissus 收录于算法学习

2021-10-08 约 4822 字预计阅读 10 分钟

二叉堆

二叉堆主要应用有两个，一种是排序方法堆排序，第二是一种数据结构–优先队列。

二叉堆概览

二叉堆就是一种特殊的二叉树（完全二叉树），只不过存储在数组中。一般的链表二叉树，操作节点的指针，而在数组中，将数组索引作为指针：

用一个图理解：

注意数组的第一个索引0空着不用。

二叉堆还分为最大堆和最小堆。最大堆的性质是：每个节点都大于等于它的两个子节点。

优先级队列

优先队列这种数据结构有一个特殊功能，插入和删除元素的时候，元素会自动排序，底层就是二叉堆实现。有两个主要的API，分别是insert插入一个元素和delMax删除最大元素。

大顶堆e代码如下：(没有使用Go语言任何内建的包)

var pq = []int{0}
// 插入元素
func insert(pq *[]int, e int) {
  	// 先把新元素加到最后
    *pq = append(*pq, e)
  	// 然后让他上浮到正确位置
    swim(*pq, len(*pq) - 1)
}
// 删除最大值
func delMax(pq *[]int) int {
  	// 堆顶就是最大元素
    max, N := (*pq)[1], len(*pq)
  	// 把这个元素换到最后，删除
    (*pq)[1], (*pq)[N - 1] = (*pq)[N - 1], (*pq)[1]
    *pq = (*pq)[:N - 1]
  	// 让pq[1]下沉到正确位置
    sink(*pq, 1)
    return max
}
// 上浮
func swim(pq []int, k int) {
    // 如果浮到堆顶，就不能再上浮了
    for k > 1 && pq[k / 2] < pq[k] {
        // 如果第k个元素比上层大，将k换上去。
        pq[k/2], pq[k] = pq[k], pq[k/2]
        k /= 2
    }
}
// 下沉
func sink(pq []int, k int) {
  	// 如果沉到堆底，就沉不下去了
    for 2*k <= len(pq) - 1 {
      	// 先假设左边节点较大
        older := 2*k
      	// 如果右边节点存在，比一下大小
        if 2*k + 1 <= len(pq) - 1 && pq[older] < pq[2*k + 1] {
            older = 2*k + 1
        }
      	// 节点k比两个子节点都大，就不必下沉
        if pq[older] < pq[k] {
            break
        }
      	// 否则，不符合最大堆的结构，下沉k节点
        pq[older], pq[k] = pq[k], pq[older]
        k = older
    }
}

实现`swim`和`sink`

对于最大堆，会破坏堆性质的有两种情况：

如果某个节点A比它的子节点中的一个小，那么A就不配做父节点，应该下去，这就对A进行下沉。
如果某个节点A比它的父节点大，那么A不应该做子节点，应该上去，就对A上浮。

上浮某个节点A，只需要A和其父节点比较大小即可。上浮代码实现：

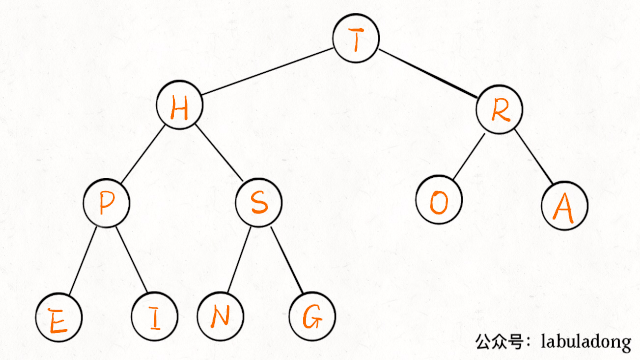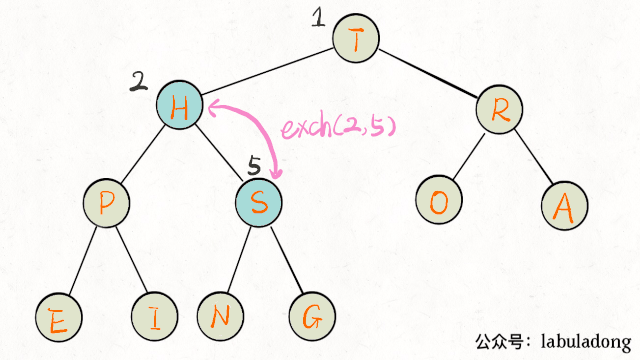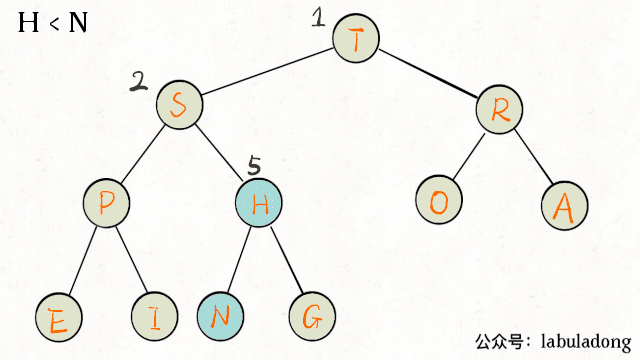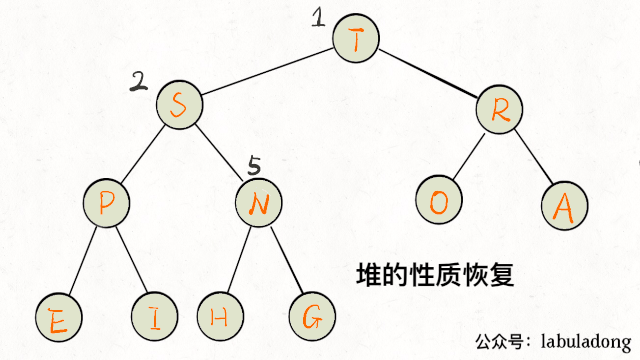
动图演示上浮过程：

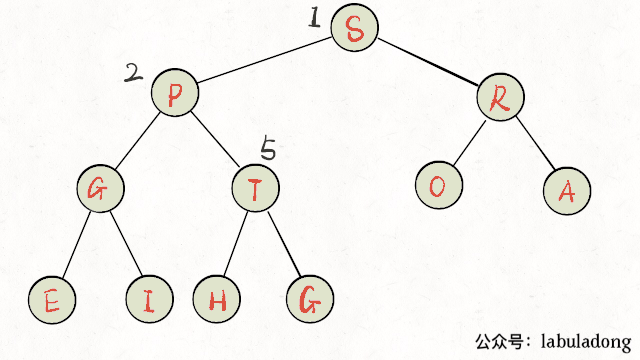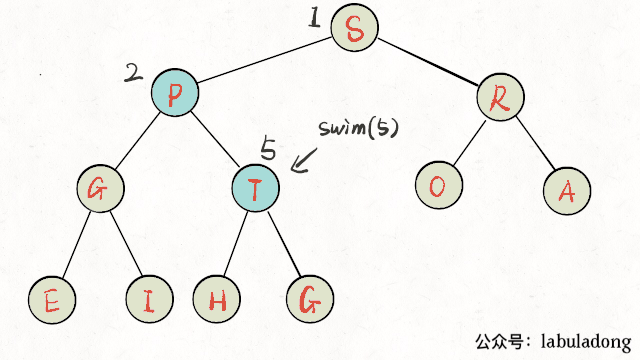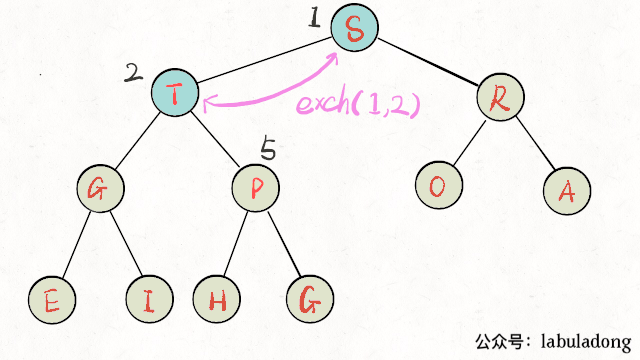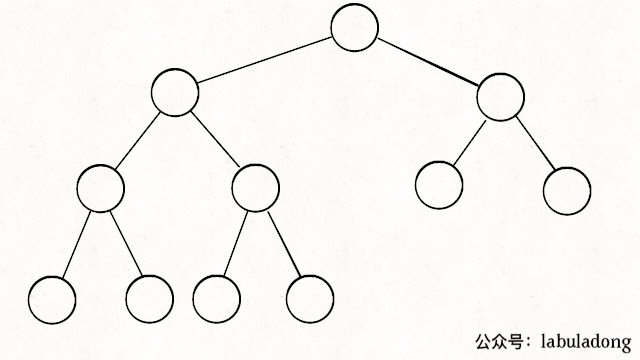
下沉某个节点A，需要A和其两个子节点比较大小，如果A不是最大的就需要调整位置，要把较大的子节点和A交换。下沉代码实现：

动图演示下沉过程：

实现`delMax`和`insert`

这两个方法是建立在swim和sink上的。

insert方法先把要插入的元素添加到堆底的最后，然后让其上浮到正确位置。代码如下：

delMax方法先把堆顶元素A和堆底最后的元素B对调，然后删除A，最后B下沉到正确位置。

使用heap包实现优先队列

heap包对任意实现了heap接口的类型提供堆操作。该接口定义如下：

可以看出，这个堆结构继承自sort.Interface,而sort.Interface需要实现三个方法：

Len() int
Less(i, j int) bool
Swap(i, j int)

再加上堆接口定义的两个方法：

Push(x interface{})
Pop() interface{}

故是要实现了这五个方法，就定义了一个堆。下面是官方文档实现的优先队列代码：

type Item struct {
    value string // item的值
    priority int // item在优先队列中的优先级
    index int // 在优先队列中的索引
}

type PriorityQueue []*Item

func (pq PriorityQueue) Len() int {
  	return len(pq)
}

func (pq PriorityQueue) Less(i, j int) bool {
  	return pq[i].priority > pq[j].priority
}

func (pq PriorityQueue) Swap(i, j int) {
  	pq[i], pq[j] = pq[j], pq[i]
  	pq[i].index = i
  	pq[j].index = j
}

func (pq *PriorityQueue) Push(x interfase{}) {
    n := len(*pq)
    item := x.(*Item)
    item.index = n
    *pq = append(*pq, item)
}

func (pq *PriorityQueue) Pop() interface{} {
  	old := *pq
  	n := len(old)
  	item := old[n - 1]
  	old[n - 1] = nil // 避免内存泄漏
  	item.index = -1 // 为了安全
  	*pq = old[0 : n-1]
  	return item
}

func main() {
	// Some items and their priorities.
	items := map[string]int{
		"banana": 3, "apple": 2, "pear": 4,
	}

	// Create a priority queue, put the items in it, and
	// establish the priority queue (heap) invariants.
	pq := make(PriorityQueue, len(items))
	i := 0
	for value, priority := range items {
		pq[i] = &Item{
			value:    value,
			priority: priority,
			index:    i,
		}
		i++
	}
	heap.Init(&pq)

	// Insert a new item.
	item := &Item{
		value:    "orange",
		priority: 1,
	}
	heap.Push(&pq, item)
}

数据流的中位数

思路分析

直接的想法就是底层用一个数组，通过插入排序保证有序，调用findMedian方法时，可以通过计算索引得出中位数，addNum搜索插入位置时可以用二分搜索算法。但是插入操作需要搬移数据，最坏时间复杂度为O(N)。链表的查找时间也是O(N)。

本题必须使用有序数据结构，本题核心思路是使用两个优先级队列。

梯形是小顶堆，但其中元素较大，称为large；倒三角是大顶堆，但是元素较小，称为small。两个堆中元素之差不能超过1。

addNum

难点是：不仅要维护large和small的元素个数之差不超过 1，还要维护large堆的堆顶元素要大于等于small堆的堆顶元素。所用技巧：想要往large里添加元素，不能直接添加，而是要先往small里添加，然后再把small的堆顶元素加到large中；向small中添加元素同理。

findMedian

只需要比较两个堆的元素数量，一样则返回堆顶元素之和除以二；不一样就返回堆元素数量多的堆顶元素。

代码实现

代码如下：

type MedianFinder struct {
    // 优先级队列
    // large是小顶堆，small是大顶堆
    large, small PriorityQueue
}

type PriorityQueue struct {
    sort.IntSlice
}

func (pq *PriorityQueue) Push(x interface{}) {
    item := x.(int)
    pq.IntSlice = append(pq.IntSlice, item)
}

func (pq *PriorityQueue) Pop() interface{} {
  	old := pq.IntSlice
  	n := len(old)
  	item := old[n - 1]
  	pq.IntSlice = old[0 : n-1]
  	return item
}

/** initialize your data structure here. */
func Constructor() MedianFinder {
    return MedianFinder{}
}


func (this *MedianFinder) AddNum(num int)  {
    if this.small.Len() >= this.large.Len() {
        heap.Push(&this.small, -num)
        heap.Push(&this.large, -heap.Pop(&this.small).(int))
    } else {
        heap.Push(&this.large, num)
        heap.Push(&this.small, -heap.Pop(&this.large).(int))
    }
}


func (this *MedianFinder) FindMedian() float64 {
    // 如果元素不一样多, 返回元素多的堆顶元素
    if this.large.Len() > this.small.Len() {
        return float64(this.large.IntSlice[0])
    } else if this.small.Len() > this.large.Len() {
        return float64(-this.small.IntSlice[0])
    }
    // 如果元素一样多，返回之和除以二
    return float64(this.large.IntSlice[0]- this.small.IntSlice[0]) / 2
}

注意：默认为小顶堆，需要重写Less()方法，才能改为大顶堆；本题为了方便使用负号这个技巧，将元素变为负再加入堆中，则小顶堆可以视为大顶堆。

addNum方法时间复杂度 O(logN)，findMedian方法时间复杂度 O(1)。

滑动窗口中的中位数

此题是上一题升级版，不仅动态增加，还动态减少。由于优先队列只支持删除堆顶元素无法删除指定元素，则采用延迟删除技巧。

延迟删除：当需要移出优先队列中的某个元素时，只将这个删除操作记录下来，而不去真的删除这个元素。当这个元素出现在堆顶时，再去将其移出对应的优先队列。

代码如下：

// 记录延迟删除的哈希表
var delayed map[int]int
var dq *DoubleQueue

func medianSlidingWindow(nums []int, k int) []float64 {
    // 双优先队列
    delayed = map[int]int{}
    dq = &DoubleQueue{}
    for _, num := range nums[: k] {
        dq.insert(num)
    }
    n := len(nums)
    result := make([]float64, 1, n - k + 1)
    result[0] = dq.getMiddle()
    for i := k; i < n; i++ {
        dq.insert(nums[i])
        dq.erase(nums[i - k])
        result = append(result, dq.getMiddle())
    }

    return result
}

// 双优先队列结构
type DoubleQueue struct {
    // small是大顶堆，large是小顶堆
    small, large PriorityQueue
}

// 因为优先队列只能堆顶删除，故采用延迟删除方式，用哈希表记录需要延迟删除的元素，当该元素
// 到堆顶时，延迟删除该元素

// 使两个优先队列元素平衡
func (dq *DoubleQueue) makeBalance() {
    // 如果无法平衡，small元素会多一个
    if dq.small.size > dq.large.size + 1 {
        dq.small.size--
        dq.large.size++
        heap.Push(&dq.large, -heap.Pop(&dq.small).(int))
        dq.small.prune()
    } else if dq.small.size < dq.large.size {
        dq.large.size--
        dq.small.size++
        heap.Push(&dq.small, -heap.Pop(&dq.large).(int))
        dq.large.prune()
    }
}

func (dq *DoubleQueue) insert(x int) {
    if dq.small.Len() == 0 || x <= -dq.small.IntSlice[0] {
        dq.small.size++
        heap.Push(&dq.small, -x)
    } else {
        dq.large.size++
        heap.Push(&dq.large, x)
    }
    dq.makeBalance()
}

func (dq *DoubleQueue) getMiddle() float64 {
    // 如果两个堆元素不一样多，返回元素多的堆顶元素
    if dq.small.size > dq.large.size {
        return float64(-dq.small.IntSlice[0])
    } else if dq.large.size > dq.small.size {
        return float64(dq.large.IntSlice[0])
    }
    // 元素一样多,相加除以2
    return float64(dq.large.IntSlice[0] - dq.small.IntSlice[0]) / 2
}

// 删除某个元素
func (dq *DoubleQueue) erase(num int) {
    delayed[num]++
    if num <= -dq.small.IntSlice[0] {
        dq.small.size--
        // 立即删除
        if num == -dq.small.IntSlice[0] {
            dq.small.prune()
        }
    } else {
        dq.large.size--
        if num == dq.large.IntSlice[0] {
            dq.large.prune()
        }
    }
    dq.makeBalance()
}

// 小顶堆
type PriorityQueue struct {
    sort.IntSlice
    // 因为有延迟删除，可能存在需要删除的元素没有删除，所以需要记录堆的实际大小
    size int
}

func (pq *PriorityQueue) Push(x interface{}) {
    pq.IntSlice = append(pq.IntSlice, x.(int))
}

func (pq *PriorityQueue) Pop() interface{} {
    old := pq.IntSlice
    item := old[len(old) - 1]
    pq.IntSlice = old[: len(old) - 1]
    return item
}

// 确保堆顶元素不是待移除元素
func (pq *PriorityQueue) prune() {
    for pq.Len() > 0 {
        num := pq.IntSlice[0]
        if pq == &dq.small {
            num = -num
        }
        if d, has := delayed[num]; has {
            if d > 1 {
                delayed[num]--
            } else {
                delete(delayed, num)
            }
            heap.Pop(pq)
        } else {
            break
        }
    }
}

把数组排成最小的数

采用堆排序，排序规则如下：

若拼接字符串 xy > yx, 则x > y。

代码如下：

func minNumber(nums []int) string {
    // 排序 -- 堆实现
    var (
        pq PriorityQueue
        result []byte
    )
    for _, val := range nums {
        heap.Push(&pq, val)
    }
    for pq.Len() != 0 {
        result = append(result, strconv.Itoa(heap.Pop(&pq).(int))...)
    }
    return string(result)
}

type PriorityQueue struct {
    sort.IntSlice
}

func(pq *PriorityQueue) Less(x, y int) bool {
    numX, numY := pq.IntSlice[x], pq.IntSlice[y]
    tempX, tempY := numX, numY
    for i := tempX; i != 0; i /= 10 {
        numY *= 10
    }
    // 特殊处理
    if numX == 0 {
        numY *= 10
    }
    numY += tempX
    for i := tempY; i != 0; i /= 10 {
        numX *= 10
    }
    if numY == 0 {
        numX *= 10
    }
    numX += tempY
    if numX < numY {
        return true
    } else {
        return false
    }
}

func (pq *PriorityQueue) Push(x interface{}) {
    pq.IntSlice = append(pq.IntSlice, x.(int))
}

func(pq *PriorityQueue) Pop() interface{} {
    old := pq.IntSlice
    n := len(old)
    item := old[n - 1]
    pq.IntSlice = old[: n-1]
    return item
}

Less(x, y int) bool方法的重写解释,当前元素对应的下标x在y后面，如果Less方法返回true，则交换x,y下标对应的元素；返回false则不交换。

快速排序

快速排序的逻辑是，若要对nums[lo..hi]进行排序，先找一个分界点p，通过交换元素使得nums[lo..p-1]都小于等于nums[p]，且nums[p+1..hi]都大于nums[p]，然后递归地去nums[lo..p-1]和nums[p+1..hi]中寻找新的分界点，最后整个数组都被排序了。

代码如下：

partition函数

索引p左侧的元素都比nums[p]小，右侧的元素都比nums[p]大，意味着这个元素已经放到了正确的位置上。递归调用会把nums[p]之外的元素也放到正确位置上。代码如下：

洗牌算法

用洗牌算法的目的：快速排序最好情况下，每次每次p都恰好是正中间(lo + hi) / 2，那么遍历的元素总数就是：N + N/2 + N/4 + N/8 + … + 1等比数列求和，求个极限就等于2N，所以遍历元素个数为2N，时间复杂度为O(N)。最坏情况下p一直都是lo + 1或者一直都是hi - 1，遍历的元素总数就是：N + (N - 1) + (N - 2) + … + 1是等差数列求和，时间复杂度会退化到O(N^2)。为了尽可能防止极端情况发生，所以需要在算法开始的时候对nums数组来一次随机打乱。

数组中第K个最大元素

二叉堆解法

二叉堆解法比较简单，由于堆大小不会超过K，所以时间复杂度是O(NlogK)，空间复杂度是O(K)。代码如下：

func findKthLargest(nums []int, k int) int {
    // 小根堆
    var pq PriorityQueue
    for _, val := range nums {
        if pq.Len() < k {
            heap.Push(&pq, val)
        } else {
            heap.Push(&pq, val)
            heap.Pop(&pq)
        }
    }
    return heap.Pop(&pq).(int)
}

type PriorityQueue struct {
    sort.IntSlice
}

func (pq *PriorityQueue) Push(x interface{}) {
    pq.IntSlice = append(pq.IntSlice, x.(int))
}

func (pq *PriorityQueue) Pop() interface{} {
    old := pq.IntSlice
    n := len(old)
    item := old[n - 1]
    pq.IntSlice = old[: n-1]
    return item
}

快速选择解法

快速选择算法比较巧妙，时间复杂度更低，是快速排序的简化版。

partition函数会将nums[p]排到正确的位置，使得nums[lo..p-1] < nums[p] < nums[p+1..hi]。那么我们可以把p和k进行比较，如果p < k说明第k大的元素在nums[p+1..hi]中，如果p > k说明第k大的元素在nums[lo..p-1]中。时间复杂度是O(N)。

代码如下：

func findKthLargest(nums []int, k int) int {
    // 快速选择算法
    shuffle(nums)
    low, high := 0, len(nums) - 1
    k = len(nums) - k
    for low <= high {
        p := partition(nums, low, high)
        if p < k {
            // 第k大元素在nums[p+1..high]中
            low = p + 1
        } else if p > k {
            // 第k大元素在nums[low..p - 1]中
            high = p - 1
        } else {
            // 找到第k大元素
            return nums[p]
        }
    }
    return -1
}

func partition(nums []int, low, high int) int {
    if low == high {
        return low
    }
    // 将nums[low]作为默认分界点pivot
    pivot := nums[low]
    i, j := low, high + 1
    for {
        // 保证nums[low..i]都小于pivot
        for i++; nums[i] < pivot; i++ {
            if i == high {
                break
            }
        }
        // 保证nums[j..high]都大于pivot
        for j--; nums[j] > pivot; j-- {
            if j == low {
                break
            }
        }
        if i >= j {
            break
        }
        // 此时有nums[i] > pivot && nums[j] < pivot
        nums[i], nums[j] = nums[j], nums[i]
    }
    // 将pivot值交换到正确位置
    nums[j], nums[low] = nums[low], nums[j]
    return j
}

func shuffle(nums []int) {
    n := len(nums)
    for i := 0; i < n; i++ {
        // 从i到最后随机选一个元素
        r := i + rand.Intn(n - i)
        nums[i], nums[r] = nums[r], nums[i]
    }
}

注意：找第K大的元素，即从小到大排序找len(nums) - k索引位置的元素。

桶排序

桶排序重要的是它的思想，而不是具体的实现。思想为：将待排序的序列分到若干个桶中，每个桶内的元素在进行个别排序。桶排序借助了桶的位置完成一次初始排序，如果划分桶的方式合理，使元素均匀的分配到各个桶中，那么时间复杂度最好是O(N)。

例如待排序序列8 5 22 15 28 9 45 42 39 19 27 47 12,可以设定放入桶编号规则为:n/10，这样右侧所有桶内数据都比左侧大，在分别对各个桶内元素排序：

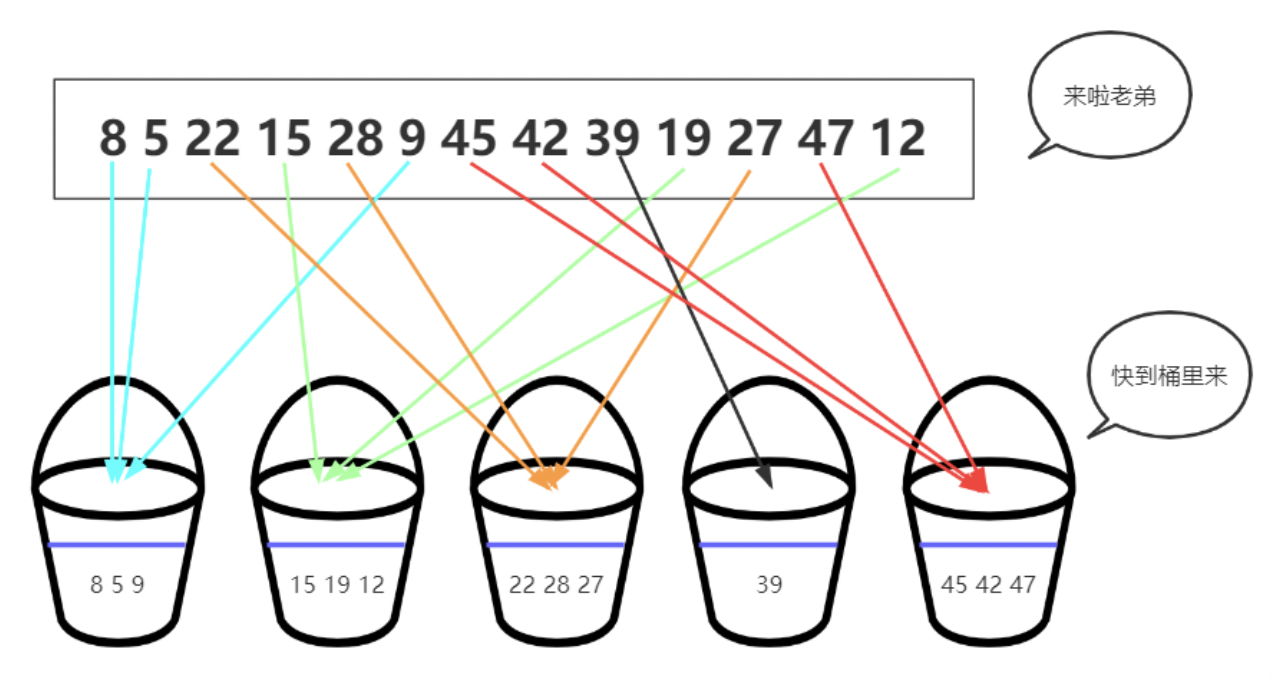
存在重复元素

本题可以使用桶排序思想，桶编号划分规则为:nums[i]/(t+1)，这样划分的目的是确保差值小于等于 t 的数能够落到一个桶中，但需要注意负数要特殊处理一下，才能划分到正确的桶编号中。这样遍历数组时，如果当前元素所在桶有元素，则必然满足<=t的条件；如果当前元素所在桶前后相邻桶有元素，可单独判断是否满足条件；其他桶内元素都不满足条件。代码如下：

func containsNearbyAlmostDuplicate(nums []int, k int, t int) bool {
    // 桶排序思想
    bucket := map[int]int{}
    for index, val := range nums {
        id := getId(val, t + 1)
        if _, ok := bucket[id]; ok {
            return true
        }
        if num, ok := bucket[id - 1]; ok && abs(num, val) <= t {
            return true
        }
        if num, ok := bucket[id + 1]; ok && abs(num, val) <= t {
            return true
        }
        // 加入桶
        bucket[id] = val
        // 删除前k范围外的元素
        if index >= k {
            delete(bucket, getId(nums[index - k], t + 1))
        }
    }
    return false
}

func getId(x, w int) int {
    if x >= 0 {
        return x / w
    }
    return (x + 1) / w - 1
}

func abs(x, y int) int {
    if x > y {
        return x - y
    }
    return y - x
}

注意：

当前元素的前k个元素外的元素所在桶可以进行删除，因为i-j>k不满足条件。

如果桶内有满足条件的元素，就会直接返回，所以桶中只会最多存在一个元素，因此用map数据结构来表示桶，提高查找效率。

目录

排序

二叉堆

二叉堆概览

优先级队列

实现swim和sink

实现delMax和insert

使用heap包实现优先队列

数据流的中位数

思路分析

代码实现

滑动窗口中的中位数

把数组排成最小的数

快速排序

数组中第K个最大元素

二叉堆解法

快速选择解法

桶排序

存在重复元素

实现`swim`和`sink`

实现`delMax`和`insert`