数学技巧

Narcissus 收录于算法学习

2021-10-01 约 840 字预计阅读 2 分钟

快速幂

根据幂运算的定义可以知道，如果要求 x 的 N 次幂，那么暴力方法就是用一个 N 次的循环，然后累乘得到结果，时间复杂度为o(N)。快速幂算法可以将复杂度降为O(logN)。

二进制拆分

以N = 10为具体场景，10写成二进制表示为1010(BIN),那么求x的10次幂，就可以写成如下式子：

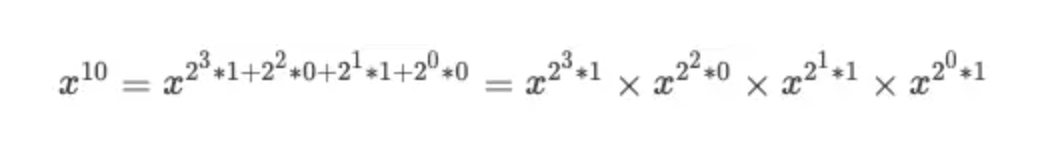
对上面的最后结果按从低位到高位交换位置如下：

在不考虑幂指数的*0和*1，只看前半部分，会有规律：左式每次是要乘以自身，就是下一项的左式。我们的例子中有：

编程思路为：从x开始维护一个左式，每一次迭代都执行x *= x，然后每次遇到右边是*1的情况，就记录以下res *= x，这样就模拟出了二进制拆分的计算思路。

编程实现

先简单实现计算出2的10次方这个例子，代码如下：

将n,x做成参数，编写一个快速幂方法，代码如下：

func qPow(x, n int) int {
	res := 1
	for n != 0 {
		if n & 1 == 1 {
			res *= x
		}
		x *= x
		n >>= 1
	}
	return res
}

复杂度

不妨设求x的N次方，并且令N的所有二进制位都是1，就有如下等式：

则k就是计算机需要计算的次数，可以反推出k的大小：

超级次方

题目要求返回幂运算a^b的计算结果与1337取模后的结果。有三个难点：

如何处理用数组表示的指数？

b是一个数组，即b可能非常大，没办法直接转换为整型。

如何得到求模之后的结果？

一般是先把幂运算结果算出来，再取模，但幂运算结果非常大，会溢出报错。

如何高效进行幂运算？

即采用快速幂算法，解决这个难点。

处理数组指数

不考虑求模要求，以b = [1,5,6,4]为例，结合指数运算法则，有以下规律：

即可以采用递归实现。

处理mod运算

由于计算机编码方式，形如(a * b) % mod这样的运算，乘法结果可能会溢出，防止溢出的技巧为：

(a*b)%k = (a%k)*(b%k) % k即对乘法结果求模，等价于先对每个因子都求模，然后对因子相乘的结果再求模。

代码如下：

const mod int = 1337

func superPow(a int, b []int) int {
    // 快速幂+递归
    if len(b) == 0 {
        return 1
    }
    last := b[len(b) - 1]
    b = b[: len(b) - 1]
    result := pow(a, last) * pow(superPow(a, b), 10)
    return result % mod
}

// 返回x的n次方求模
func pow(x, n int) int {
    res := 1
    for n != 0 {
        if n & 1 == 1 {
            res *= x % mod
        }
        x *= x % mod
        n >>= 1
    }
    return res % mod
}

目录