图论

Narcissus 收录于算法学习

2021-12-20 约 1769 字预计阅读 4 分钟

图论基础

1. 图的逻辑结构和具体实现

一幅图是由节点和边构成的，逻辑结构如下：

实现上，通常用邻接表和邻接矩阵来实现。

邻接表很直观，就是每个节点x的邻居都存在一个列表里，然后把x和这个列表关联起来；邻接矩阵则是一个二维布尔数组，如果节点x和y是相连的，就把matrix[x][y]=true。

邻接表好处就是占用空间少，但是无法快速判断两个节点是否相邻。

2. 图的遍历

图的遍历和多叉树类似，最大的区别是图可能包含环，因此需要一个visited数组进行辅助。遍历框架如下：

3. 题目实践

代码如下：

func allPathsSourceTarget(graph [][]int) [][]int {
    // dfs
    var (
        ans [][]int
        dfs func(now int)
    )
    n := len(graph)
    track := make([]int, 0, n)
    track = append(track, 0)
    dfs = func(x int) {
        if x == n-1 {
            ans = append(ans, append([]int(nil), track...))
            return 
        }
        for _, v := range graph[x] {
            track = append(track, v)
            dfs(v)
            track = track[:len(track)-1]
        }
    }
    dfs(0)
    return ans
}

二分图

二分图简介

二分图是一种特殊的图模型，定义如下:

二分图的顶点集可分割为两个互不相交的子集，图中每条边依附的两个顶点都分属于这两个子集，且两个子集内的顶点不相邻。

二分图就是双色问题，即用两种颜色将图中的所有顶点着色，且使得任意一条边的两个端点的颜色都不相同。

算法4中的应用例子为如何存储电影演员和电影之间的关系？

如果用哈希表存储，则需要两个哈希表分别存储两种映射关系；如果用图结构存储，就可以用到二分图模型。

2. 例题

二分图的判定

使用DFS遍历判定代码如下：

func isBipartite(graph [][]int) bool {
    // dfs 顶点着色
    n := len(graph)
    // 0表示未被访问，1、-1表示两种颜色
    color := make([]int, n)
    ok := true
    var dfs func(x int)
    dfs = func(x int) {
        for _, v := range graph[x] {
            if color[v] == 0 {
                // 相邻节点没有被访问
                color[v] = -1 * color[x]
                dfs(v)
            } else {
                // 被着色
                if color[v] == color[x] {
                    ok = false
                }
            }
        }
    }

    for x := 0; x < n; x++ {
        if color[x] == 0 {
            color[x] = 1
            dfs(x)
        }
    }
    return ok
}

LeetCode 886 代码省略

并查集（Union-Find）

并查集算法主要是解决图论中动态连通性的问题。

只有路径压缩的并查集复杂度是 O(logn) 的，这也是大多数情况下的实现方案；只有启发式合并（按深度合并）的并查集的复杂度也是 O(logn) 的，适用于可持久化的场景。

1. 基本介绍

用森林来表示图的动态联通性，用数组来实现森林。设定树的每一个节点都有一个指向父节点的指针，如果是根节点则指向自己。

如果两个节点连通，则它们一定拥有相同的根节点；如果某两个节点被连通，则让其中任意一个节点的根节点接到另一个节点的根节点上。

2. 路径压缩

普通方式可能会出现极端的情况，即树变成了链表，只有路径压缩的并查集时间复杂度才是O(logN)。

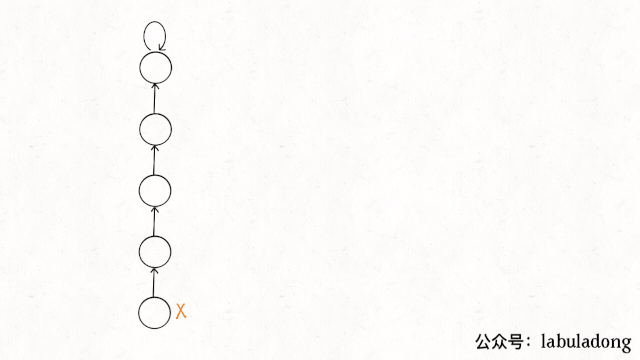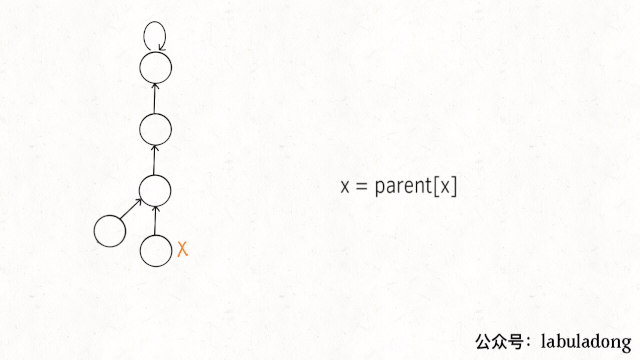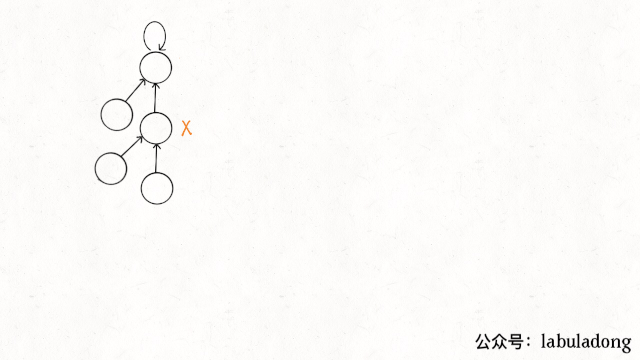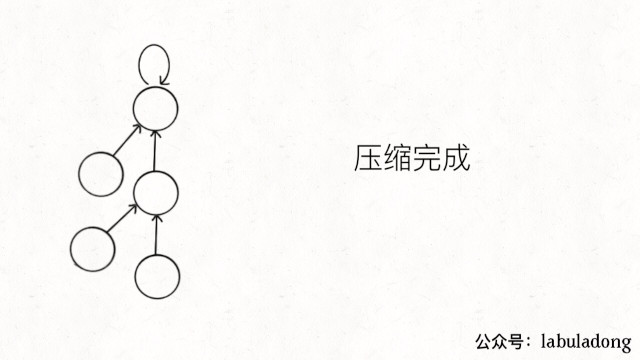
实现上只需要在find()方法中加一行代码：

注意：除了采用路径压缩的方式，优化并查集复杂度为O(logn)，采用启发式合并(按深度合并)的方式也可以，即使用额外的数组size来记录每一个节点的深度，每次合并将深度小的树接到深度大的树上面。

3. 代码实现

注意：上述路径压缩是采用迭代方式实现，下述代码采用递归方式实现。

var fa []int
initUF := func(n int) {
  fa = make([]int, n)
  for i := range fa {
    fa[i] = i
  }
}
initUF(n + 1)
// 查询节点的根节点
var find func(int) int
find = func(x int) int {
  if fa[x] != x {
    // 路径压缩递归写法
    fa[x] = find(fa[x])
  }
  return fa[x]
}
// 连通两个节点
union := func(from, to int) {
  fa[find(from)] = find(to) 
}
// 判断是否连通
connected := func(x, y int) bool {
  return find(x) == find(y)
}

注意:也可以用结构体的方式实现

4. 并查集应用

拓扑排序

1. 概述

拓扑排序针对有向无环图，如果存在环，则必定循环依赖，无法进行拓扑排序。

2. 两种方式

该方式需要用到入度表作为辅助，将入度为0的节点加入队列中进行广度优先遍历，每一次遍历后将节点入度值减一。

该方式借助标记列表vis，共有三种值表示某个节点的三种状态：

vis[i]==0表示该节点未被访问；

vis[i]==1表示该节点被当前节点启动的DFS访问；

vis[i]==-1表示该节点被其他节点启动的DFS访问。

注意：后序遍历结果反转才是拓扑排序的结果

3. 例题

BFS方式代码

func findOrder(numCourses int, prerequisites [][]int) []int {
    // 广度搜索-需要额外的入度数组
    graph := make([][]int, numCourses)
    indeg := make([]int, numCourses)
    var result []int
    for _, prerequisite := range prerequisites {
        graph[prerequisite[1]] = append(graph[prerequisite[1]], prerequisite[0])
        // 统计入度
        indeg[prerequisite[0]]++
    }
    var queue []int
    for x := 0; x < numCourses; x++ {
        if indeg[x] == 0 {
            queue = append(queue, x)
        }
    }
    for len(queue) != 0 {
        cur := queue[0]
        queue = queue[1:]
        result = append(result, cur)
        for _, v := range graph[cur] {
            indeg[v]--
            if indeg[v] == 0 {
                queue = append(queue, v)
            }
        }
    }
    if len(result) != numCourses {
        return []int{}
    }
    return result
}

DFS方式代码

func findOrder(numCourses int, prerequisites [][]int) []int {
    // 拓扑排序
    // 构建入度邻接矩阵
    graph := make([][]int, numCourses)
    for _, r := range prerequisites {
        graph[r[1]] = append(graph[r[1]], r[0])
    }
    // 0表示未被访问，-1表示被访问，1表示当前轮被访问
    vis := make([]int, numCourses)
    result := make([]int, 0, numCourses)
    ok := false
    var dfs func(x int)
    dfs = func(x int) {
        vis[x] = 1
        for _, v := range graph[x] {
            if vis[v] == -1 {
                continue
            }
            if vis[v] == 1 {
                ok = true
                return
            }
            dfs(v)
          	// 剪枝
            if ok {
                return
            }
        }
        vis[x] = -1
        result = append(result, x)
    }

    for x := 0; x < numCourses; x++ {
        if vis[x] == 0 {
            dfs(x)
        }
    }
    // 存在环
    if ok {
        return []int{}
    }
    // 反转后续遍历
    for i, j := 0, numCourses-1; i < j; i, j = i+1, j-1 {
        result[i], result[j] = result[j], result[i]
    }
    return result
}

目录

图论